Benchmark: Lid-driven Cavity (2d)

This is a classic benchmark for incompressible Navier-Stokes solvers. The domain is a unit square box, comprising 3 no-slip walls (code 500), and the top "wall" moving with a unit horizontal velocity,no vertical component (code 503). The lid is non-leaky (at the top corner nodes, u=0,v=0 is prescribed). To determine the relative pressure field, a single prescibed value may be needed (semi-implicit only). In which case, P=0 is applied at node 1. This is a forced convection problem, covering a range of Reynolds numbers.

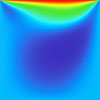
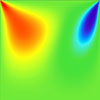
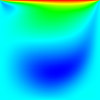
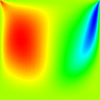
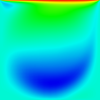
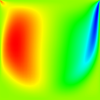
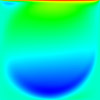
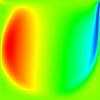
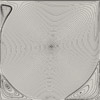
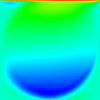
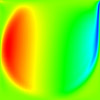
The results for a simple non-uniform structured mesh are presented below. The results are compared to data from Ghia et al (1982) JCP 48:387-411. The horizontal velocity is plotted along the vertical mid-line, with the square datapoints from Ghia et al. Vertical and horizontal contour plots are also provided, along with streamtracer results using ParaView post-processing.

The Input zip file contains only the files necessary to run the specified program, the All zip file also contains the output and values extracted from Ghia et al 1982 paper.